Assignment 8

姓名	学号	学院	专业
米家龙	18342075	计算机学院	软件工程

• Assignment 8
  • 要求
    • 测试用例
    • 题目
  • 解答
    • 1. 输入条件的自然语义陈述
    • 2. 输出结果的自然语义陈述
    • 3. 判定规则 & 推理演算过程
      • 第6列
        • 第6列判定规则
        • 第6列推演过程
      • 第23列
        • 第23列判定规则
        • 第23列推演过程

要求

测试用例

设计处理单价为5角的饮料的自动售货机软件的测试用例。软件规格说明如下：

1. 操作者投入5角或1元的硬币，按下橙汁或啤酒的按钮，售货机送出相应的饮料 (不考虑饮料不足的情况)。
2. 若售货机没有零钱找，则一个显示零钱找完 的红灯亮。
   • 此时操作者投入1元硬币并按下按钮后，不送出饮料，而是退还1元硬币。
3. 若售货机有零钱找，则显示零钱找完 的红灯灭。
   • 此时操作者投入1元硬币并按下按钮后，售货机送出饮料，退还5角硬币。

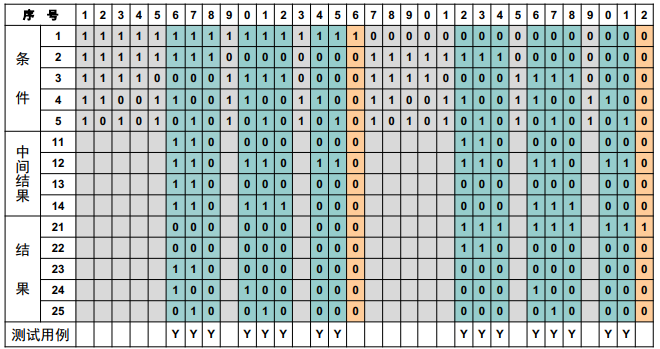
题目

分析 Chap.5 (Lec.19) 自动售货机软件例子生成的判定表图例的第6列和第23列，分别给出：

1. 输入条件的自然语义陈述；
2. 输出结果的自然语义陈述；
3. 用命题逻辑形式描述实现上述输入-输出过程所应用的判定规则，并写出获得输出结果的推理演算过程。

解答

1. 输入条件的自然语义陈述

原因清单（输入条件）：

• $C_1$：售货机可找零
• $C_2$：投入1元硬币
• $C_3$：投入5角硬币
• $C_4$：按下橙汁按钮
• $C_5$：按下啤酒按钮

第6列：

\[C_1 \ \text{售货机可找零} \rightarrow C_2 \ \text{投入1元硬币} \rightarrow C_4 \ \text{按下}{\color{orange}{\bf{橙汁}}}\text{按钮}\]

第23列：

\[\overline{C_1} \ \text{售货机无零可找} \rightarrow C_2 \ \text{投入1元硬币} \rightarrow C_5 \ \text{按下}{\color{orange}{\bf{啤酒}}}\text{按钮}\]

2. 输出结果的自然语义陈述

结果清单（输出结果）：

• $E_{21}$：零钱找完灯亮
• $E_{22}$：退还1元硬币
• $E_{23}$：退还5角硬币
• $E_{24}$：送出橙汁饮料
• $E_{25}$：送出啤酒饮料

第6列：

\[E_{23} \ \text{退还5角硬币} \rightarrow E_{24} \text{送出}{\color{orange}{\bf{橙汁}}}\text{饮料}\]

第23列：

\[E_{21} \ {\color{orange}{\bf{零钱找完}}} \text{灯亮} \rightarrow E_{22} \text{退还1元硬币}\]

3. 判定规则 & 推理演算过程

第6列

第6列判定规则

\[\begin{aligned} C_4 \vee C_5 & \Rightarrow T_{12} \\ C_2 \wedge T_{12} & \Rightarrow T_{11} \\ C_1 \wedge T_{11} & \Rightarrow T_{13} \\ C_3 \vee T_{13} & \Rightarrow T_{14} \\ T_{13} & \Rightarrow E_{23} \\ C_4 \wedge T_{14} & \Rightarrow E_{24} \end{aligned}\]

第6列推演过程

以 $C_1$, $C_2$, $C_4$ 为前提，应用上述规则得到：

\[\begin{aligned} T_{12} & = C_4 \vee C_5 = 1 \\ T_{11} & = C_2 \wedge T_{12} = 1 \\ T_{13} & = C_1 \wedge T_{11} = 1 \\ T_{14} & = C_3 \vee T_{13} = 1 \\ E_{23} & = T_{13} = 1 \\ E_{24} & = C_4 \wedge T_{14} = 1 \end{aligned}\]

由此证明 $E_{23}$ 和 $E_{24}$

第23列

第23列判定规则

\[\begin{aligned} C_4 \vee C_5 & \Rightarrow T_{12} \\ C_2 \wedge T_{12} & \Rightarrow T_{11} \\ \overline{C_1} & \Rightarrow E_{21} \\ \overline{C_1} \wedge T_{11} & \Rightarrow E_{22} \end{aligned}\]

第23列推演过程

以 $\overline{C_1}$, $C_2$, $C_5$ 为前提，应用上述判定规则得到：

\[\begin{aligned} T_{12} & = C_4 \vee C_5 = 1 \\ T_{11} & = C_2 \wedge T_{12} = 1 \\ E_{21} & = \overline{C_1} = 1 \\ E_{22} & = \overline{C_1} \wedge T_{11} = 1 \end{aligned}\]

由此证明 $E_{21}$ 和 $E_{22}$